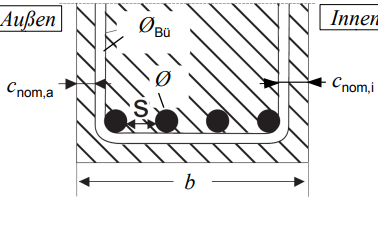
Balken Bewehrung

Hinweis: Randabstände liegen im Scheitel der Biegung des Bügels
$θ$ Durchmesser Längsstab
$θ_{B ü}$ Durchmesser Bügel
$D_{B ü}$ Biegerollendurchmesser Bügel
mit $θ_{B ü} < 20 m m : D_{B ü} = 4 \cdot θ_{B ü} s o n s t D_{B ü} = 7 \cdot θ_{B ü}$
$s_{m i n}$ Mindest-Längsstababstand
mit $θ_{m i n} < 20 m m : s_{m i n} = 20 m m s o n s t s_{m i n} = θ$
$c_{n o m, a}$ Betondeckung außen
$c_{n o m, i}$ Betondeckung innen
Berechnung der maximalen Zahl ”n” der Stäbe im Balkenquerschnitt
$T e r m 1 = b - c_{n o m, a} - c_{n o m, i}$ $T e r m 2 = - 2 \cdot θ_{B ü} - (1 - \frac{1}{\sqrt{2}}) \cdot D_{B ü}$ $T e r m 3 = - \frac{1}{\sqrt{2}} \cdot θ - θ - s_{m i n}$ $T e r m 4 = θ + s_{m i n}$ $n = G a n z z a h l [\frac{T e r m 1 + T e r m 2 + T e r m 3}{T e r m 4}] + 2$

Anzahl an Stäben: n = 0

Randbedingungen
$b$ $=$ 0 $c m,$ $c_{n o m, a}$ $=$ 0 $c m,$ $c_{n o m, i}$ $=$ 0 $c m,$
$θ_{B ü}$ $=$ 0 $c m,$ $θ$ $=$ 0 $c m,$
Zwischenergebnisse
$D_{B ü}$ $=$ 0 $c m,$ $s_{m i n}$ $=$ 0 $c m,$
Maximalen Zahl ”n” der Stäbe im Balkenquerschnitt
$T e r m 1 = b - c_{n o m, a} - c_{n o m, i}$ $T e r m 2 = - 2 \cdot θ_{B ü} - (1 - \frac{1}{\sqrt{2}}) \cdot D_{B ü}$ $T e r m 3 = - \frac{1}{\sqrt{2}} \cdot θ - θ - s_{m i n}$ $T e r m 4 = θ + s_{m i n}$ $n = G a n z z a h l [\frac{T e r m 1 + T e r m 2 + T e r m 3}{T e r m 4}] + 2$ $n =$ 0

Allgemeine Konstruktionshinweise